Как определить силу тяги двигателя. Примеры решения задач

Задача 1

Автомобиль может разгоняться до 216 км/ч. Максимальная мощность двигателя равна 96 кВт. Определите максимальную силу тяги двигателя.

Решение

Переведем киловатты в ватты, а километры в час — в метры в секунду:

\(96\;\times\;1000=96000\;Вт\)

\(\frac{216\times1000}{3600}=60\frac мс\)

\(F_т\;=\;\frac N v = \frac{96000}{60} = 1600 Н\)

Задача 2

Троллейбус весом 12 тонн за 5 секунд проезжает по горизонтальной дороге 10 метров. Сила трения равна 2,4 кН. Определите силу тяги, которую развивает двигатель.

Решение

Переведем тонны в килограммы, а килоньютоны в ньютоны:

\(12\;\times\;1000=12000\;кг\)

\(2,4\;\times\;1000=2400\;Н\)

\(F_т-\;F_{тр}=m\;\times\;a\), следовательно, \(F_т=m\times a\;+\;F_{тр}\)

Чтобы определить ускорение а, воспользуемся формулой \(s\;=\;\frac{at^2}2\)

Подставив численные значения величин, получаем:

\(a\;=\;\frac{2s}{t^2}^{}=\frac{20}{25}\;=\;0,8\)

\(F_т=\;12000\times0,8\;+\;2400\;=\;12000\;Н\;=\;12\;кН\)

Задача 3

Транспорт, весящий 4 тонны, едет в гору. Уклон — 1 метр на каждые 25 метров пути. \(\mu\) — 0,1 от силы тяжести, \(а = 0\). Определите силу тяги.

Решение

Начертим схему:

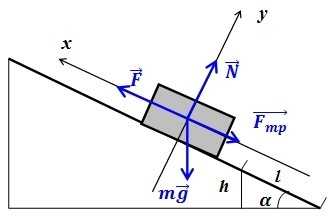
\(m\times g\;+\;N\;+\;F_{тр\;}+\;F_т\;=\;m\times a\)

Сделаем проекции на координатные оси:

\(OX: -\;mg\;\times\;\sin\alpha\;-\;F_{тр\;}+\;F_т\;=\;0\)

\(OY: N\;-\;mg\;\times\;\cos\alpha\;=\;0 => N\;=\;mg\;\times\;\cos\alpha\;\)

\(F_{тр}\;=\;\mu N\;=\;\mu mg\;\times\;\cos\alpha\)

Подставим значение \(F_{тр}\) в уравнение \(OX\) и определим \(F_т\):

\(-mg\;\times\;\sin\alpha\;-\;\mu\)

\(mg\;\times\;\cos\alpha\;+\;F_т\;=\;0\)

\(=> F\;=\;mg\;\left(\sin\alpha\;+\;\mu\;\times\;\cos\alpha\right)\)

Найдем синус и косинус \(\alpha\), подставим их в общую формулу:

\(\sin\alpha\;=\;\frac hl\;=\;\frac1{25}\)

\(\cos\alpha\;=\;\frac{\sqrt{l^{2\;}-\;h^2}}l\;\)

Примеры решения задач

Задание. На автомобиль имеющий массу 1 т при его движении по горизонтальной поверхности, действует сила трения, которая равна =0,1 от силы тяжести. Какой будет сила тяги, если автомобиль движется с ускорением 2 м/с?

Решение. Сделаем рисунок.

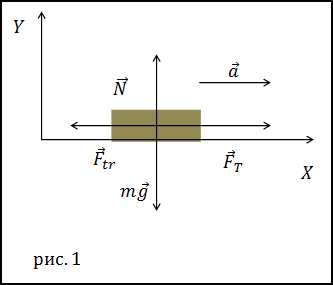
В качестве основы для решения задачи используем второй закон Ньютона:

Спроектируем уравнение (1.1) на оси X и Y:

По условию задачи:

Подставим правую часть выражения (1.4) вместо силы трения в (1.2), получим:

Переведем массу в систему СИ m=1т=10 3 кг, проведем вычисления:

Ответ. F_T=2,98 кН

Задание. На гладкой горизонтальной поверхности лежит доска массой M. На доске находится тело массы m. Коэффициент трения тела о доску равен . К доске приложена сила горизонтальная сила тяги, которая зависит от времени как: F=At (где A=const). В какой момент времени доска начнет выскальзывать из-под тела?

Решение. Сделаем рисунок.

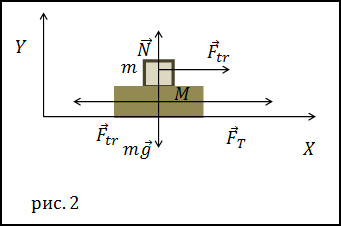
Для решения задачи нам потребуются проекции сил на осиX и Y, которые отличны от нуля. Для тела массы m:

Для тела массы M:

Обозначим момент времени, в который доска начнет выскальзывать из-под тела t, тогда

Ответ.

Мощность двигателя

Расчет мощности двигателя автомобиля

5 популярных способа как вычислить мощность двигателя автомобиля используя такие данные как: — обороты двигателя, — объем мотора, — крутящий момент, — эффективное давление в камере сгорания, — расход топлива, — производительность форсунок, — вес машины — время разгона до 100 км.

Каждая из формул, по которой будет производиться расчет мощности двигателя автомобиля довольно относительная и не может со 100% точностью определить реальную лошадиную силу движущую машину. Но произведя подсчеты каждым из приведенных гаражных вариантов, опираясь не те или иные показатели, можно рассчитать, по крайней мене, среднее значение будь-то стоковый или тюнингованный движок, буквально с 10-ти процентной погрешностью. Мощность — энергия, вырабатываемая двигателем, она преобразуется в крутящий момент на выходном валу ДВС. Это не постоянная величина. Рядом со значениями максимальной мощности всегда указываются обороты, при которых можно её достигнуть. Точкой максимума достигается при наибольшем среднее эффективном давлении в цилиндре (зависит от качества наполнения свежей топливной смесью, полноты сгорания и тепловых потерь). Наибольшую мощность современные моторы выдают в среднем при 5500–6500 об/мин. В автомобильной сфере измерять мощность двигателя принято в лошадиных силах. Поэтому поскольку большинство результатов выводятся в киловаттах вам понадобится калькулятор перевода кВт в л.с

Как рассчитать мощность через крутящий момент

Самый простой расчет мощности двигателя авто можно определить по зависимости крутящего момента и оборотов. —Крутящий момент Сила, умноженная на плечо ее приложения, которую может выдать двигатель для преодоления тех или иных сопротивлений движению. Определяет быстроту достижения мотором максимальной мощности. Расчетная формула крутящего момента от объема двигателя: Мкр = VHхPE/0,12566, где VH – рабочий объем двигателя (л), PE – среднее эффективное давление в камере сгорания (бар). —Обороты двигателя — Скорость вращения коленчатого вала. Формула для расчета мощности двигателя внутреннего сгорания автомобиля имеет следующий вид: P = Mкр * n/9549 , где: Mкр – крутящий момент двигателя (Нм), n – обороты коленчатого вала (об./мин.), 9549 – коэффициент, дабы обороты подставлять именно в об/мин, а не косинусами альфа. Поскольку по формуле, результат получим у кВт, то при надобности также можно конвертировать в лошадиные силы или попросту умножать на коэффициент 1,36. Использование данных формул — это самый простой способ перевести крутящий момент в мощность. А дабы не вдаваться во все эти подробности быстрый расчет мощности ДВС онлайн, можно произвести, используя наш калькулятор. Но, к сожалению, данная формула отражает лишь эффективную мощность мотора которая не вся доходит именно до колес автомобиля. Ведь идут потери в трансмиссии, раздаточной коробке, на паразитные потребители (кондиционер, генератор, ГУР и т.п.) и это без учета таких сил как сопротивление качению, сопротивление подъему, аэродинамическое сопротивление.

Примеры решения задач

Задание. На автомобиль имеющий массу 1 т при его движении по горизонтальной поверхности, действует сила трения, которая равна

=0,1 от силы тяжести. Какой будет сила тяги, если автомобиль движется с ускорением 2 м/с?

Решение. Сделаем рисунок.

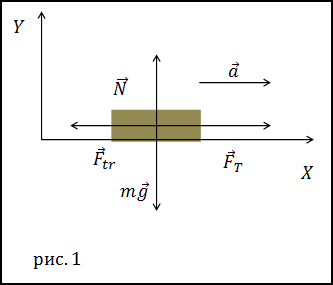
В качестве основы для решения задачи используем второй закон Ньютона:

Спроектируем уравнение (1.1) на оси X и Y:

Подставим правую часть выражения (1.4) вместо силы трения в (1.2), получим:

Переведем массу в систему СИ m=1т=10 3 кг, проведем вычисления:

Ответ. FT=2,98 кН

Псс.. Ты хочешь зарабатывать на маркетплейсах?

Узнай, какой товар пользуется спросом, поставь его на маркетплейс и начни зарабатывать! Переходите по моей ссылке и получите бесплатный доступ к системе аналитики! По промокод VASILIK50 скидка 50% на любой тариф!

Вы можете увидеть, как зарабатывает тот или иной продавец, сколько раз и на какую сумму продался каждый конкретный товар. Оценить ниши в целом и многое другое. В системе есть обучение, проводятся вебинары.

Попробуйте. По моей ссылке будет бесплатный доступ на несколько дней. Жмите СЮДА

Источник

Трение качения

Про колесо совершенно точно нельзя сказать, что оно скользит или покоится. При этом сила трения явно возникает, так как существует соприкосновение двух поверхностей.

В этом случае мы говорим о трении качения — сопротивлению движения, если одно тело катится по поверхности другого. При равных силах нормального давления сила трения скольжения больше силы трения качения. Это явление часто используют, например, ставя колесики на чемодан. Да и вообще, ставя колесики куда угодно.

Сила трения качения Fтр = λN/R Fтр — сила трения качения λ — коэффициент трения N — сила реакции опоры R — радиус колеса

Задачи на трение качения встречаются только в задачах высокого уровня сложности (например, в олимпиадах). Однако на формулу посмотреть полезно, даже если вы не планируете покорять самую высокую вершину.

Если приглядеться, она очень похожа на формулу трения скольжения, только в знаменателе появляется радиус. Если мы будем увеличивать знаменатель, то сила трения будет уменьшаться. То есть, чем больше радиус колеса, тем меньше трение.

Ладно, давайте все-таки решим задачу на силу трения качения — только никому об этом не рассказывайте

Задача

Какого радиуса понадобится установить колесо, чтобы уменьшить силу трения, равную 17 Н — на 5 Н. При коэффициенте трения 0,6 мм и силе нормального давления тела равной 10 кН.

Решение:

Берем формулу силы трения качения:

Fтр = λN/R

Выражаем из нее радиус:

R = λN/Fтр

Коэффициент трения и сила нормального давления нам даны, а чтобы найти силу трения, нам нужно вычесть из начальной силы трения ее изменение:

Fтр2 = Fтр1 — ΔFтр = 17 — 5 = 12Н

Подставляем числа в формулу, предварительно переведя их в СИ:

СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».

R = λN/Fтр = 0,0006 *10000/12 = 0,5 м

Ответ: необходимо поставить колесо радиусом 0,5 м.

Первый закон механики

Некоторое время в физике никто не подвергал сомнению мысль Аристотеля, высказанную им в работе «Механика»: «Движущееся тело останавливается, если сила, толкающая его, прекращает свое действие».

Это ошибочное утверждение, опирающееся на обыденное восприятие явлений природы, впервые опроверг Галилей, сделавший важнейший для науки вывод о вечности, неуничтожаемости движения.

Анализируя движение шарика по наклонной плоскости (рис. 2.1), он писал: «…скорость, которую однажды сообщили телу, будет строго сохранятся, поскольку устранены внешние причины ускорения и замедления, — условие, которое обнаруживается только на горизонтальной плоскости, ибо в случае движения по наклонной плоскости вниз уже существует причина ускорения, в то время как при движении по наклонной плоскости вверх налицо замедление; из этого следует, что движение по горизонтальной плоскости вечно, ибо, если скорость будет постоянной, движение не может быть уменьшено или ослаблено, а тем более уничтожено».

Этот фундаментальный вывод Г. Галилея использовал И. Ньютон в своем знаменитом труде «Математические начала натуральной философии» (1687 г.) при формулировании первого закона динамики (закона инерции):

Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, поскольку оно не принуждается приложенными силами изменить это состояние.

А. Эйнштейн и Л. Инфельд в работе «Эволюция физики» проще сформулировали этот закон: «Всякое тело сохраняет состояние покоя или равномерного прямолинейного движения, если только оно не вынуждено изменить его под влиянием действующих сил».

Тело большой массы сложнее разогнать до некоторой скоро сти, чем тело малой массы, так как оно более инертно.

Движение шарика по наклонной плоскости рассматривали относительно поверхности Земли, которая считалась неподвижной. Итак, первый закон динамики установлен для систем отсчета, считающихся неподвижными или движущихся относительно последних прямолинейно, равномерно и поступательно. Такие системы называются инерциальными. Инертность тел проявляется в сохранении ими своего состояния покоя или прямолинейного равномерного движения до того времени, пока какая-нибудь внешняя причина не выведет их из этого состояния.

Тело большой массы сложнее разогнать до некоторой скоро сти, чем тело малой массы, так как оно более инертно.

Сущность инертности, которая свойственна всем телам, заключается в том, что для изменения скорости тела необходимо взаимодействие с другим телом. Из двух взаимодействующих тел более инертно то, которое медленнее изменяет свою скорость.

Теоретически инерциальных систем отсчета может быть много, поскольку всегда можно представить тела, которые пребывают в состоянии покоя или движутся равномерно и прямолинейно (без ускорения), и связать с ними соответствующее количество систем координат и устройств для отсчета времени (часов).

Понятие инерциальной системы отсчета является научной абстракцией. В реальной жизни таких систем нет, поскольку в природе не существует абсолютно неподвижных тел (например, тело, которое неподвижно относительно Земли, вращается вместе с ней вокруг земной оси, вокруг Солнца и т. д.).

При решении задач динамики систему отсчета связывают с реальным телом, например Землей или Солнцем.

Поэтому при решении задач динамики систему отсчета связывают с реальным телом. Тогда она может рассматриваться как инерциальная с той или иной степенью приближения.

Так, например, при решении задач в небесной механике и космонавтике с высокой степенью точности инерциальной можно считать гелиоцентрическую систему с началом отсчета на Солнце и осями, направленными на некоторые звезды. Для решения большинства технических задач в качестве инерциальной берут систему отсчета, жестко связанную с Землей.

Третий закон механики

Согласно утверждению Ньютона сила является следствием взаимодействия двух или большего количества тел. Если одно тело действует на другое, то обязательно и второе тело действует на первое, т. е. если есть действие, то есть и противодействие. Понятия действия и противодействия условны, поскольку каждое из них может быть и тем и другим. Возьмем две одинаковые по мае-

се тележки и к одной из них прикрепим плоскую пружину, сжатую прочной нитью. Другую тележку поставим так, чтобы она касалась этой пружины (рис. 2.7, а).

Если нитку, которой сжата пружина, отпустить или поджечь, то пружина распрямится и обе тележки придут в движение. Это означает, что они приобрели ускорение:

Поскольку масса тележек одинакова, то одинаковы их ускорения и расстояния, которые они проходят за определенное время.
Если на одну из тележек положить некоторый груз (увеличить ее массу) и повторить опыт (рис. 2.7, б), то тележка, которая имеет большую массу, пройдет меньшее расстояние.

Таким образом, при взаимодействии двух тел соотношение модулей их ускорений равно обратному соотношению их масс:

Ускорения взаимодействующих тел имеют противоположные направления, поэтому в векторной форме можно записать

Произведение массы тела на его ускорение равно приложенной к телу силе. — сила, которая действует на первое тело со стороны второго, a  — сила, действующая на второе тело со стороны первого. Итак,

Это равенство и является математическим выражением третьего закона механики. Ньютон его сформулировал так:

действию всегда есть равное и противоположное противодействие; действия двух тел друг на друга равны между собой и направлены в противоположные стороны.

Существует и такая формулировка: любое действие одного тела на другое имеет характер взаимодействия; силы, с которыми взаимодействуют тела, всегда одинаковы и противоположно направлены.

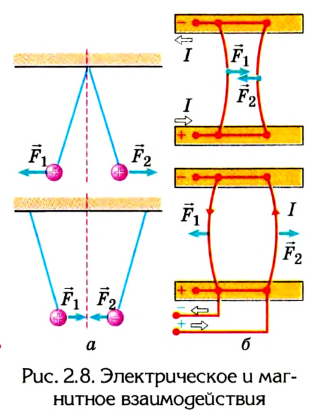
Опыты подтверждают, что силы любой природы во время взаимодействия тел возникают попарно, имеют противоположные направления и одинаковы по модулю. На рисунке 2.8 показаны электрическое (а) и магнитное (б) взаимодействия, а на рисунке 2.9 — взаимодействия в случае возникновения в телах силы упругости (имеют электромагнитную природу).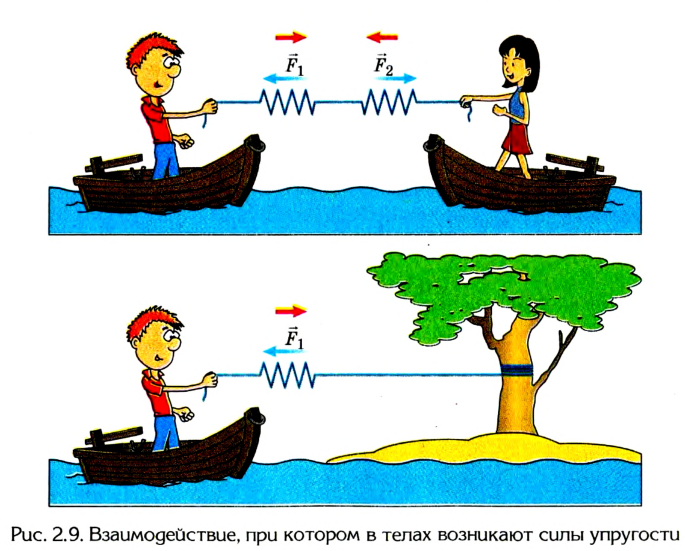

В третьем законе механики речь идет о силах, приложенных к разным телам. Поэтому, нельзя считать, что сумма сил, приложенных к каждому из взаимодействующих тел, равна нулю. Равнодействующую сил можно находить лишь в том случае, когда силы приложены к одному телу.

Сила: что это за величина

В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.

Сила — это физическая векторная величина, которая воздействует на данное тело со стороны других тел.

Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.

Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.

Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.

Второй закон механики

Второй закон механики Ньютона устанавливает взаимосвязь между кинематическими и динамическими величинами. Чаще всего он формулируется так: ускорение, которое приобретает тело под действием силы, прямо пропорционально силе, обратно пропорционально массе тела и имеет то же направление, что и сила:

где — ускорение, — равнодействующая сил, действующих на тело, Н; m — масса тела, кг.  

Если по этой формуле определить силу то получим второй закон динамики в иной формулировке: сила, действующая на тело, равна произведению массы тела и ускорения, сообщенного этой силы Второй закон механики Ньютона:

И. Ньютон сформулировал второй закон механики несколько иначе, воспользовавшись понятием количества движения (импульса тела).

Импульс или количество движения (от лат. impulsus — удар, толчок) — произведение массы тела на его скорость — одна из мер механического движения: Импульс (количество движения) — величина векторная.

Поскольку ускорение 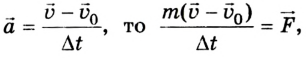отсюда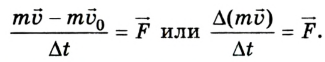
 

Изменение количества движения тела пропорционально действующей силе и происходит в направлении той прямой, вдоль которой эта сила действует.
По Ньютону второй закон механики звучит так: изменение количества движения тела пропорционально приложенной движущей силе и происходит в направлении той прямой, по которой эта сила действует.

Действие силы не порождает само движение, а лишь изменяет его; сила вызывает изменение скорости (ускорение), а не саму скорость.
Второй закон механики Ньютона обобщил исключительно важный факт: действие силы не порождает само движение, а лишь изменяет его; сила вызывает изменение скорости (ускорение), а не саму скорость.

Заказать решение задач по физике

Трение покоя

Если вы решите сдвинуть с места грузовик, вряд ли у вас это получится. Не то, чтобы мы в вас не верим — просто это невозможно сделать из-за того, что масса человека во много раз меньше массы грузовика, да еще и сила трения мешает это сделать. Мир жесток, что тут поделать.

В случае, когда сила трения есть, но тело не двигается с места, мы имеем дело с силой трения покоя.

Сила трения покоя равна силе тяги. Например, если вы пытаетесь сдвинуть с места санки, действуя на них с силой тяги 10 Н, то сила трения будет равна 10 Н.

Сила трения покоя Fтр = Fтяги Fтр — сила трения скольжения Fтяги — сила тяги

Немного потренируемся!

Задача

Найти силу трения покоя для тела, на которое действуют сила тяги в 4 Н.

Решение:

Тело покоится, значит

Fтр = Fтяги = 4 Н

Ответ: сила трения равна 4 Н.

Тяга реактивного двигателя самолета

Сила тяги двигателя, или его движущая сила, равноценна всем силам давления воздуха на внутреннюю поверхность силовой установки. Тяга некоторых видов реактивных двигателей зависит от скорости и высоты полета. Для вычисления силы тяги реактивного двигателя часто приходится определять тягу на конкретной высоте, у земли, на взлете и во время какой-либо скорости. Для ЖРД сила тяги равноценна произведению массы исходящих газов на скорость, с которой они вылетают из сопла двигателя.

Для ВРД (воздушно-реактивный двигатель) сила тяги измеряется как результат массы газов на разность скоростей, а именно скорости воздушной струи, выходящей из сопла двигателя, и скорости поступающего воздуха в двигатель. Проще говоря, данная скорость уравнивается к скорости полета самолета с реактивным двигателем. Тяга ВРД обычно измеряется в тоннах или килограммах. Важным качественным показателем ВРД является его удельная тяга. Для турбореактивного двигателя – тяга, отнесенная к конкретной единице веса воздуха, который проходит через двигатель в секунду. Этот показатель позволяет понять, насколько высока эффективность эксплуатации воздуха в двигателе для образования тяги. Удельная тяга измеряется в килограммах тяги на 1 кг воздуха, расходуемого за секунду. В некоторых случаях применяется другой показатель, который также называется удельной тягой, показывающей отношение количества топлива, которое расходуется, к силе тяги за секунду. Естественно, что чем выше показатель удельной тяги ВРД, тем меньше поперечный вес и размеры самого двигателя.

Показатель полетной или тяговой мощности – это сила, которая задействует реактивный двигатель при конкретной скорости полета. Как правило, измеряется в лошадиных силах. Величина лобовой тяги говорит о степени конструктивного оптимума реактивного двигателя. Лобовая тяга – это отношение наибольшего показателя площади поперечного сечения к тяге. Лобовая тяга равна тяге, в кг поделенной на площадь в метрах квадратных.

В мировой авиации наиболее ценится тот двигатель, который обладает высокой лобовой тягой.

Чем совершеннее ВРД в конструктивном отношении, тем меньший показатель его удельного веса, а именно общий вес двигателя вместе с приборами и обслуживающими агрегатами, поделенный на величину собственной тяги.

Реактивные двигатели, как и тепловые вообще, отличаются друг от друга не только по мощности, весу, тяге и другим показателям. При оценивании ВРД огромную роль играют параметры, которые зависят от собственной экономичности, а именно от КПД (коэффициент полезного действия). Среди данных показателей главным считается удаленный расход топлива на конкретную единицу тяги. Он выражается в килограммах топлива, которое расходуется за час на образование одного килограмма тяги.
 

Действие силы тяги

Множество сил, действующих на движущийся объект, для упрощения вычислений делят на две группы: силу тяги и силы сопротивления.

Её прекращение

Когда действие силы тяги прекращается, движущееся тело замедляется и постепенно останавливается, так как на него воздействуют силы, мешающие продолжать двигаться, например, трение.

1 закон Ньютона о действии

Согласно этому закону в формулировке самого Ньютона, любое тело остается в покое или равномерно движется по прямой, пока на него не воздействуют силы, заставляющие его изменить это состояние.

В современной физике в формулировку внесены уточнения:

• закон применим только в системах отсчета, называемых инерциальными;
• тело может вращаться на месте, не находясь под воздействием внешних сил, поэтому вместо термина «тело» следует использовать термин «материальная точка».

Чтобы переместить неподвижный предмет, на него должна воздействовать некая сила. Чтобы изменить скорость движения предмета, также необходимо воздействие силы, замедляющей его или ускоряющей. Так как предметы обладают разной массой и соответственно разной инертностью, силы, достаточные для эффективного воздействия, тоже будут различаться.

Состояние ускорения после воздействия силы тяги

Когда движение равномерное, сила тяги и сила трения совершают одинаковую работу, уравновешивая друг друга. Воздействие силы на тело в направлении движения придает ему ускорение. Если направить ту же силу в противоположном направлении, она замедлит движение тела, что можно назвать отрицательным ускорением.

Крутящий момент и лошадиная сила

Автолюбители нередко дискутируют друг с другом: чей двигатель мощнее. Но иногда и не представляют при этом, из чего складывается данный параметр. Общепринятый термин «лошадиная сила» был введён изобретателем Джеймсом Уаттом в XVIII веке.  Он придумал его, наблюдая за лошадью, которая была запряжена в поднимающий уголь из шахты механизм. Он рассчитал, что одна лошадь за минуту может поднять 150 кг угля на высоту 30-ти метров. Одна лошадиная сила эквивалентна 735,5 Ватт, или 1 кВт равен 1,36 л.с.

В первую очередь, мощность любого мотора оценивают в лошадиных силах, и лишь потом вспоминают о крутящем моменте. Но эта тяговая характеристика тоже даёт представление о конкретных тягово-динамических возможностях автомобиля. Крутящий момент является показателем работы силового агрегата, а мощность – основным параметром выполнения этой работы. Эти показатели тесно связаны друг с другом. Чем больше производится двигателем лошадиных сил, тем больше и потенциал крутящего момента. Реализуется этот потенциал в реальных условиях через трансмиссию и полуоси машины. Соединение этих элементов вместе и определяет, как именно мощность может переходить в крутящий момент.

Простейший пример – сравнение трактора с гоночной машиной. У гоночного болида лошадиных сил много, но крутящий момент требуется для увеличения скорости через редуктор. Чтобы такая машина двигалась вперёд, надо совсем немного работы, потому что основная часть мощности используется для развития скорости.

Что касается трактора, то у него может быть мотор с таким же рабочим объёмом, который вырабатывает столько же лошадиных сил. Но мощность в этом случае используется не для развития скорости, а для выработки тяги (См. тяговый класс). Для этого она пропускается через многоступенчатую трансмиссию. Поэтому трактор не развивает высоких скоростей, зато он может буксировать большие грузы, пахать и культивировать землю, и т.д.

В двигателях внутреннего сгорания сила передаётся от газов сгорающего топлива поршню, от поршня – передаётся на кривошипный механизм, и далее на коленчатый вал. А коленвал, через трансмиссию и приводы, раскручивает колёса.

Естественно, крутящий момент двигателя не постоянен. Он сильней, когда на плечо действует бо́льшая сила, и слабей – когда сила слабнет или перестаёт действовать. То есть, когда водитель давит на педаль газа, то сила, воздействующая на плечо, повышается, и, соответственно увеличивается крутящий момент двигателя.

Мощность обеспечивает преодоление всевозможных сил, которые мешают двигаться автомобилю. Это и сила трения в двигателе, трансмиссии и в приводах автомобиля, и аэродинамические силы, и силы качения колёс и т.д. Чем больше мощность, тем большее сопротивление сил машина сможет преодолеть и развить большую скорость. Однако мощность – сила не постоянная, а зависящая от оборотов мотора. На холостом ходу мощность одна, а на максимальных оборотах – совершенно другая. Многими автопроизводителями указывается, при каких оборотах достигается максимально возможная мощность автомобиля.

Необходимо учитывать, что максимальная мощность не развивается сразу. Автомобиль стартует с места практически при минимальных оборотах (немного выше холостого хода), и для того, чтобы отмобилизировать полную мощность, требуется время. Тут и вступает в дело крутящий момент двигателя. Именно от него и будет зависеть, за какой отрезок времени автомашина достигнет своей максимальной мощности – то есть, динамика её разгона.

Зачастую водитель сталкивается с такими ситуациями, когда требуется придать автомобилю значительное ускорение для выполнения необходимого маневра. Прижимая педаль акселератора в пол, он чувствует, что автомобиль ускоряется слабо. Для быстрого ускорения нужен мощный крутящий момент. Именно он и характеризует приёмистость автомобиля.

Основную силу в двигателе внутреннего сгорания вырабатывает камера сгорания, в которой воспламеняется топливно-воздушная смесь. Она приводит в действие кривошипно-шатунный механизм, а через него – коленчатый вал. Рычагом является длина кривошипа, то есть, если длина будет больше, то и крутящий момент тоже увеличится.

Однако увеличивать кривошипный рычаг до бесконечности невозможно. Ведь тогда придётся увеличивать рабочий ход поршня, а вместе с ним и размеры двигателя. При этом уменьшатся и обороты двигателя. Двигатели с большим рычагом кривошипного механизма можно применить только лишь в крупномерных плавательных средствах. А в легковых автомашинах с небольшими размерами коленчатого вала не поэкспериментируешь.

Темы по физике

• Кинематика (19)
• Динамика и статика (32)
• Гидростатика (5)

Молекулярная физика (25)

Уравнение состояния (3)
Термодинамика (15)
Броуновское движение (6)
Прочие формулы по молекулярной физике (1)
Колебания и волны (22)
Оптика (9)

Геометрическая оптика (3)
Физическая оптика (5)
Волновая оптика (1)
Электричество (39)
Атомная физика (15)
Ядерная физика (3)

Темы по математике

• Квадратный корень, рациональные переходы (1)
• Квадратный трехчлен (1)
• Координатный метод в стереометрии (1)
• Логарифмы (1)
• Логарифмы, рациональные переходы (1)
• Модуль (1)
• Модуль, рациональные переходы (1)
• Планиметрия (1)
• Прогрессии (1)
• Производная функции (1)
• Степени и корни (1)
• Стереометрия (1)
• Тригонометрия (1)
• Формулы сокращенного умножения (1)

Сообщение от администратора:

Ребята! Кто давно хотел выучить английский?Переходите по моей ссылке и получите два бесплатных урока в школе английского языка SkyEng! Занимаюсь там сам – очень круто. Прогресс налицо.

В приложении можно учить слова, тренировать аудирование и произношение.

Попробуйте. Два урока бесплатно по моей ссылке! Жмите СЮДА

Силу тяги можно определить через полезную мощность, и скорость транспортного средства (v):

Для автомобиля, поднимающегося в горку, которая имеет уклон , масса автомобиля m сила тяги (F_T) войдет в уравнение:

где a – ускорение, с которым движется автомобиль.

Мощность через массу авто и время разгона до «сотни»

Расчет с применением веса автомобиля и его скорости разгона до 100 км/ч – один из самых простых методов вычисления реальной мощности двигателя, ведь масса авто и заявленное время разгона до «сотни» – паспортные параметры машины.

Этот метод актуален для двигателей, работающих на любых видах топлива – бензин, дизельное топливо, газ – ведь он учитывает лишь динамику разгона.

При расчете стоит учитывать вес транспортного средства вместе с водителем. Также чтобы максимально приблизить результат вычислений к действительному, стоит учесть и потери, затрачиваемые на торможение, пробуксовку, а также скорость реакции коробки передач. Играет роль и тип привода. Например, переднеприводные автомобили теряют на старте около 0,5 секунды, заднеприводные – от 0,3 секунды до 0,4 секунды.

Остается найти в сети калькулятор для расчета мощности авто через скорость разгона, внести необходимые данные и получить ответ. Нет смысла приводить математические расчеты, которые производит калькулятор, из-за их сложности.

Результат вычислений будет одним из самых точных, приближенных к реальному.

Данный метод расчета реальной мощности машины многие считают самым удобным, ведь автовладельцам придется приложить минимум усилий – измерить для чистоты эксперимента скорость разгона до 100 км/ч и внести дополнительные данные в автоматический калькулятор.

Работа и мощность

Теперь остановимся на таком понятии как «работа», которое в данном контексте имеет особое значение. Работа совершается всякий раз, когда сила — любая сила — вызывает движение. Работа равна силе, умноженной на расстояние. Для линейного движения мощность выражается как работа в определённый момент времени.

Если мы говорим о вращении, мощность выражается как вращающий момент (T), умноженный на частоту вращения (w).

Частота вращения объекта определяется измерением времени, за которое определённая точка вращающегося объекта совершит полный оборот. Обычно эта величина выражается в оборотах в минуту, т.е. мин-1 или об/мин. Например, если объект совершает 10 полных оборотов в минуту, это означает, что его частота вращения: 10 мин-1 или 10 об/мин.

Итак, частота вращения измеряется в оборотах в минуту, т.е. мин-1.

Приведем единицы измерения к общему виду.

Для наглядности возьмём разные электродвигатели, чтобы более подробно проанализировать соотношение между мощностью, вращающим моментом и частотой вращения. Несмотря на то, что вращающий момент и частота вращения электродвигателей сильно различаются, они могут иметь одинаковую мощность.

Например, предположим, что у нас 2-полюсный электродвигатель (с частотой вращения 3000 мин-1) и 4-полюсной электродвигатель (с частотой вращения 1500 мин-1). Мощность обоих электродвигателей 3,0 кВт, но их вращающие моменты отличаются.

Таким образом, вращающий момент 4-полюсного электродвигателя в два раза больше вращающего момента двухполюсного электродвигателя с той же мощностью.

Как образуется вращающий момент и частота вращения?

Теперь, после того, как мы изучили основы вращающего момента и скорости вращения, следует остановиться на том, как они создаются.

В электродвигателях переменного тока вращающий момент и частота вращения создаются в результате взаимодействия между ротором и вращающимся магнитным полем. Магнитное поле вокруг обмоток ротора будет стремиться к магнитному полю статора. В реальных рабочих условиях частота вращения ротора всегда отстаёт от магнитного поля. Таким образом, магнитное поле ротора пересекает магнитное поле статора и отстает от него и создаёт вращающий момент. Разницу в частоте вращения ротора и статора, которая измеряется в %, называют скоростью скольжения.

Скольжение является основным параметром электродвигателя, характеризующий его режим работы и нагрузку. Чем больше нагрузка, с которой должен работать электродвигатель, тем больше скольжение.

Помня о том, что было сказано выше, разберём ещё несколько формул. Вращающий момент индукционного электродвигателя зависит от силы магнитных полей ротора и статора, а также от фазового соотношения между этими полями. Это соотношение показано в следующей формуле:

Сила магнитного поля, в первую очередь, зависит от конструкции статора и материалов, из которых статор изготовлен. Однако напряжение и частота тока также играют важную роль. Отношение вращающих моментов пропорционально квадрату отношения напряжений, т.е. если подаваемое напряжение падает на 2%, вращающий момент, следовательно, уменьшается на 4%.

Формулы для определения силы тяги

Согласно второму закону Ньютона, сумма сил, воздействующих на движущееся тело, равна массе (m), умноженной на ускорение (a). Универсальной формулы, подходящей для любого сочетания сил, не существует. Чаще всего силу тяги находят с помощью общей формулы( F_т-;F_{с}=m;times;a), где (F_т) — сила тяги, (F_{с}) — силы сопротивления.При решении конкретной задачи силы, воздействующие на тело, схематически изображают в виде векторов. На схеме:

• сила тяжести mg;
• сила реакции опоры (N);
• сила трения( F_{тр});
• сила тяги (F). 

При нахождении тела на горизонтальной поверхности сила тяжести и сила реакции опоры уравновесят друг друга. Но если транспортное средство движется в гору или под гору, придется учесть влияние уклона. Тогда формула может выглядеть так: (F_т-;F_с-;mg;times;sinalpha=m;times;a.)

Работа A, которую должна совершить сила тяги, сдвигая тело, связана с ней соотношением (A;=;F;times;s). (s) здесь — расстояние, на которое тело переместилось.

Формула через мощность

Полезную механическую мощность (N) можно вычислить по формуле (N=F_т;times;v), где (v) — скорость. Для определения силы тяги нужно разделить мощность на скорость: (F_т;=;frac N v.)